までの時間が16分なので、2回目に出会う 時間は16×3=48分。 (2) 2回目に出会うまでに、はろ美さんはすく男 君よりも1152m多く進んでいるので、速さの 差は1152÷48=24m。 速さの和は2400÷16=150mなので、和差 算で考えていけば、はろ美さんの速さは (150+24)÷2 速さ × 時間 = 距離 この問題では、速さがわかっています。時間については、「弟の出発の10分後に兄が出発」ということしかわかりません。しかも、距離については、何もわかりません。この状態では、解ける気がしませんね。 頻出の計算問題です。以下の関係が成り立つことを利用して様々な移動に関する問題を解いていきます。 $$距離 = 速さ times 時間tag{1}$$ 式(1)を変形すると、以下の式が導き出されます。 $$時間 = frac{距離}{速さ}tag{2}$$ 時間の式(2)の導き方を詳しく

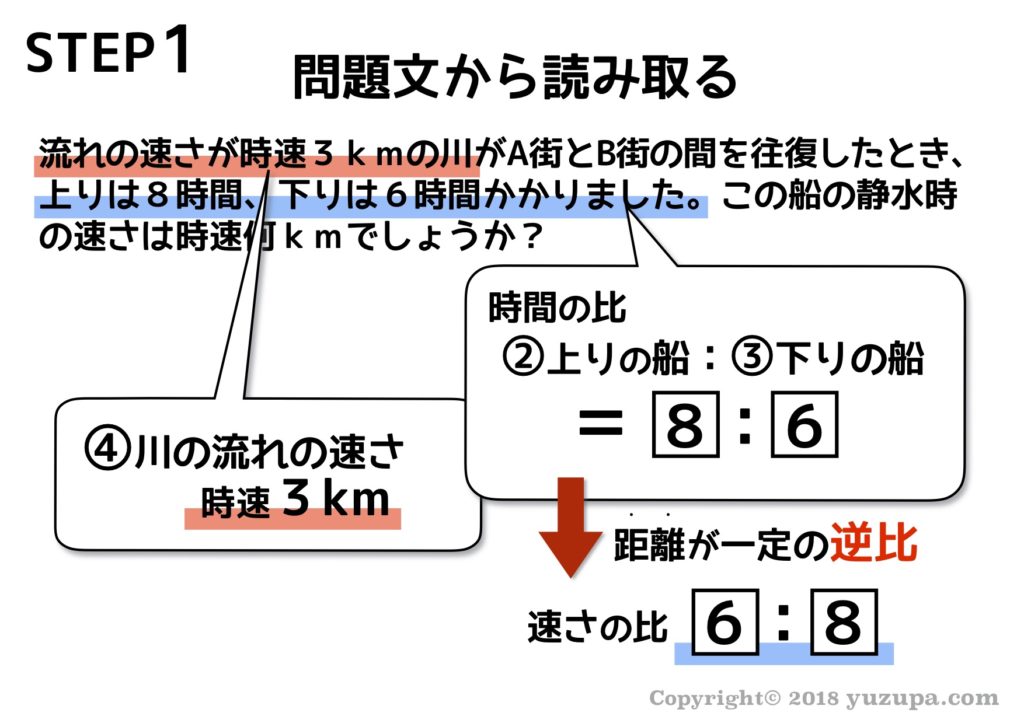
時間の比と速さの比 なぜ逆にするんですか Clear
速さ 距離 時間 追いつく
速さ 距離 時間 追いつく-方程式の文章題(速さ の問題) 方程式をたてて求めよ。 (1) A君はいつも毎分70mの速さで歩いて学校へ行く。今日は家を出るのがいつもより9分遅かったので 毎分100mの速さで走っていったらいつもと同じ時刻に学校に着いた。A君の家から学校までは何mか。 速度と距離の問題(1次方程式) 方程式を利用して問題を解くときには、問題文の中のどれかひとつの量を として、他の量を を使って表し、それらの量の関係を満たす方程式をつくります。 速度(速さ)と距離(道のり)、時間の関係は次のようになり




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
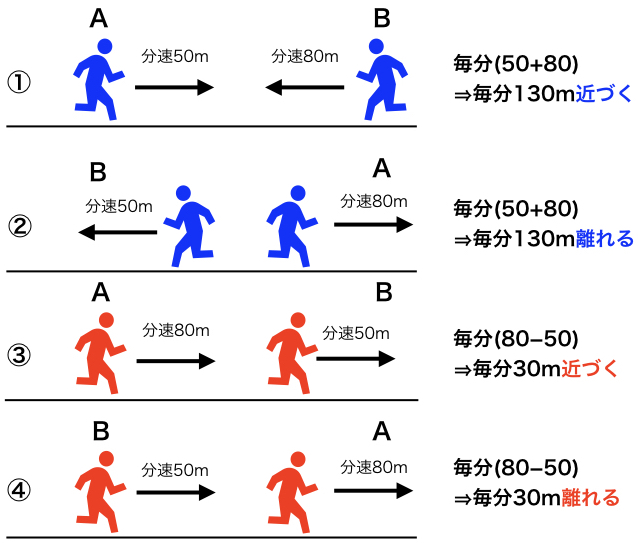
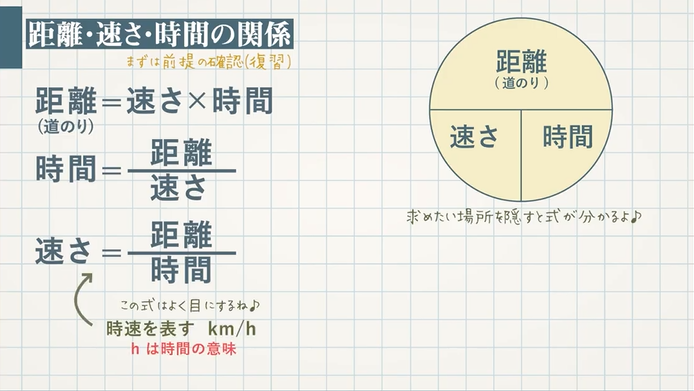
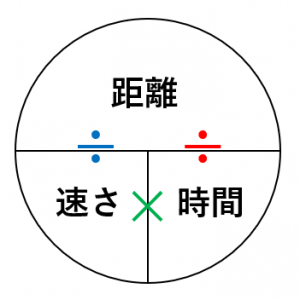
両方とも考え方は同じです。 二人が出会う(追いつく)ということは 二人のあいだの距離がゼロになる ということです。 いまある二人のあいだの距離がゼロになるまでにかかる時間を求めるのですから、「かかる時間=距離(道のり)÷速さ」という速さの3公式のひとつを使います。時間の比と速さの比を比較するのが一番速い! 比 かかるはずだった時間をx分とおけば、実際にかかった時間は(x – 5)分。 走る距離は一定で、速さの比が10 12 = 5 6なので、かかった時間の比は6 5。 x (x – 5)= 6 5;道のり=速さ×時間 速さ=道のり÷時間 時間=道のり÷速さ ただこれらはわざわざ覚える必要はなく、簡単に導出可能です。 たとえば 割合 の時と同じように長方形に当てはめれば、3つの公式は自然と導けます。 割合の3つの公式の覚え方と使い方
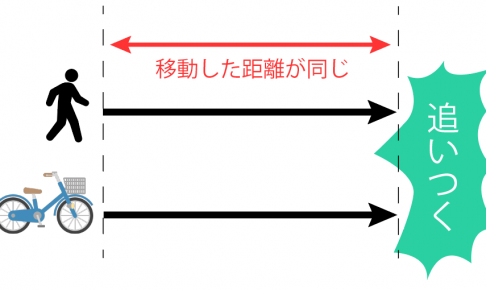
以上より、5x = 6(x – 5) 二人の速さに差があると必ず追いつくことになります。 このときの二人の速さと出発してから追いつくまでの時間や進んだ距離などの進行状況を考えていきます。 例題2) 600m先を分速35mの速さで歩いている弟を、お兄ちゃんが分速65mの速さで追いかけます。出会うまでの時間を求めるには、二人の速さを足し、表に数字を当てはめて計算します。 (14 x) × 48 = 10 m = (14 x) = 10 ÷ 48 = (14 x) = 25 x = 25 − 14 x = 11 分速 11 m
追いかける場合にかかる時間は、 時間 = 距離 ÷ (Bの速度 - Aの速度)より 10 ÷ (60 - 40) = 60分になる。 妹のすすむ距離と時間 姉が出発した時間を0とする y = 50*10 50x 1 姉のすすむ距離と時間 y = 70x 2 2式を1に代入 70x = 50*10 50x 70x 50x = 500 x = 500 x=25 姉の出発時間に加える。 旅人算は頭の体操としては覚えてよいかもしれません。同じ向きに進んで追いつくまでの時間=2人の間の道のり÷速さの差 速さの差=2人の間の道のり÷同じ向きに進んで追いつくまでの時間 2人の間の道のり=速さの差×同じ向きに進んで追いつくまでの時間 と、覚えてしまう人もいます。
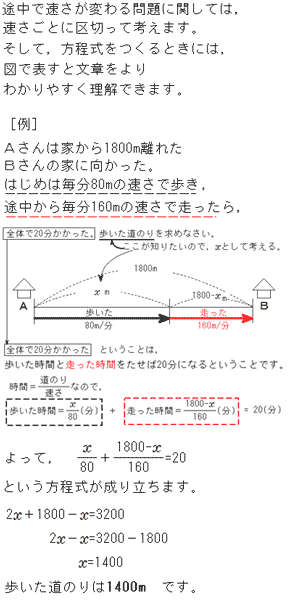



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座
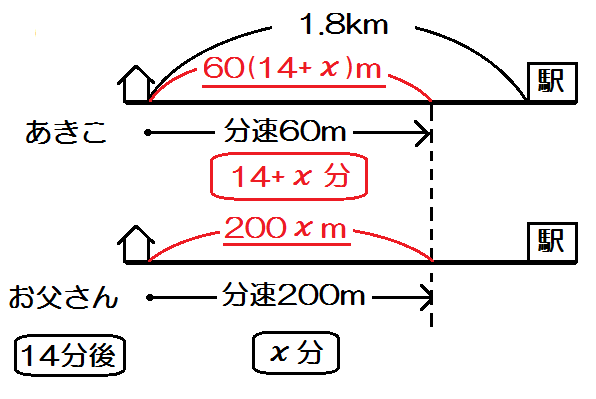



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
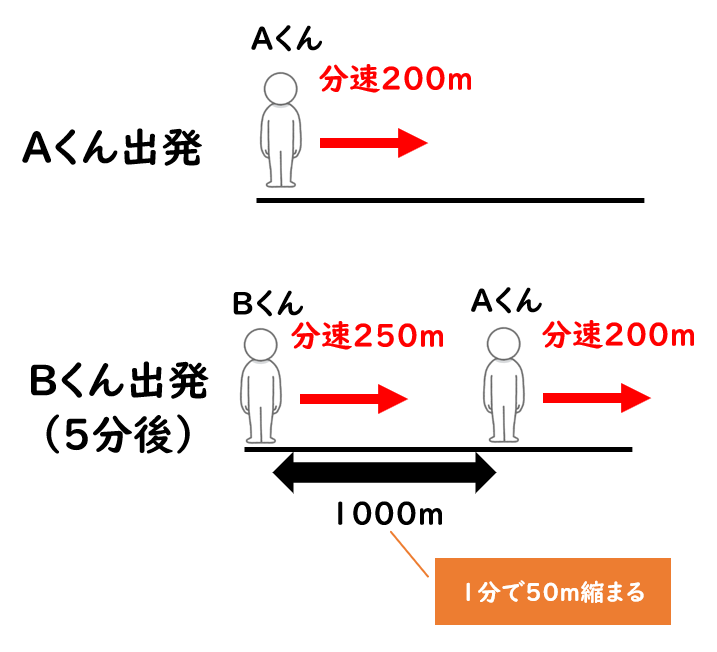
時間,距離,速さは,物理学的には速さ=距離/時間 の関係を持つ が,その関係概念はどのように形成される のだろうか。Piaget(1946a, b)以来い くつ かの研究がな されてきたが,松田 ・.・谷・松田 (19由,Matsuda (1991, 1994)が指摘するように 旅人算追いつく問題の解き方まとめ! お疲れ様でした! 2人が追いつくという問題を解くためには、2人の道のりが縮まっていくという発想が大切です。 2人の速さを見比べると、1分間でどれくらいずつ道のりが縮まるのかが分かります。 方程式(速さ)追いつく問題解き方 問題 兄が家を出発してから12分後に弟が家を出発して、兄を追いかけました。 兄の進む速さが分速60m、弟の進む速さが分速1mのとき、弟は家を出発してから何分後に兄に追いつくか。 それでは、上の




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




時間 距離 速さ 数的推理 通過算 追いつく 公務員試験道場
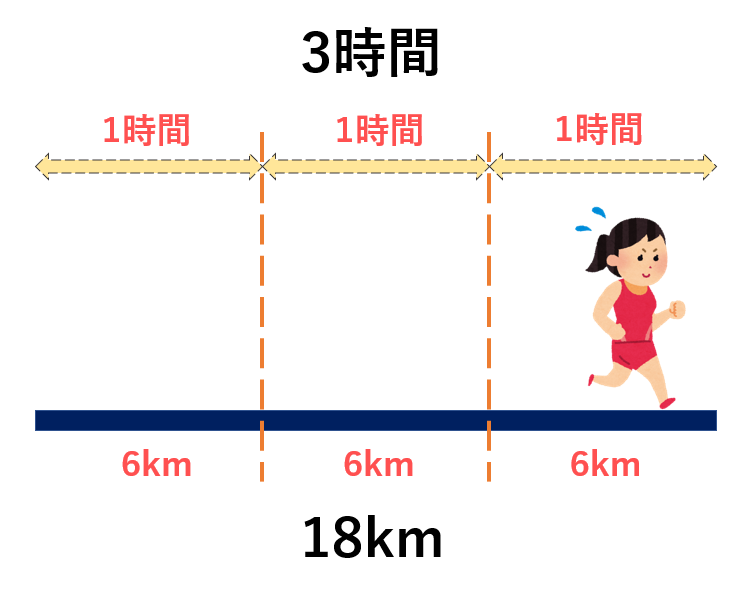
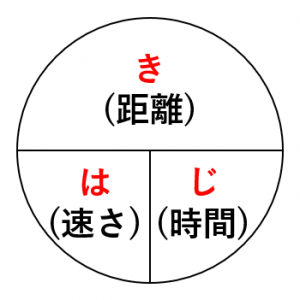
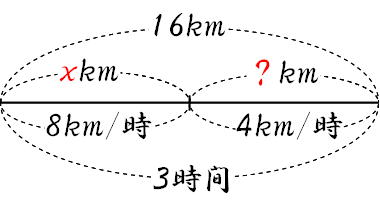
→追いつく時間=2人の間の距離÷2人の速さの差 分= 800m÷40m 父が出発したのは、次郎君が出発した10分後(7時10分)ですので、速さを求めたいときには、 速さ=距離 ÷ 時間 という公式を使います。 例えば、距離 30 k m の道のりを、 3 時間かけて進んだときの速さは、 距離 ÷ 時間 = 30 ÷ 3 = 10 つまり、 時速 10 k m です。 公式を忘れても、はじきの図で求めたいものを隠すことで解答 (1)兄が家を出発してから弟に追いつくまでの時間を x 分とする。 2人の進んだ距離を数式で表し、等式を立てる。 弟 兄 速さ 60(m/分) 210(m/分) 時間
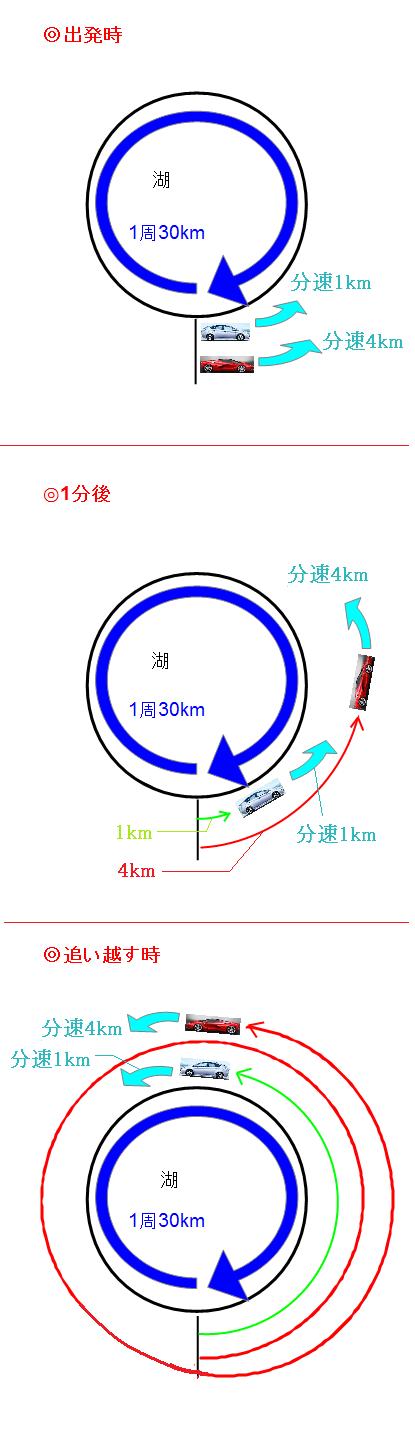



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




予習シリーズ第18 19回 旅人算 の予習 日々の学習 妹中学受験
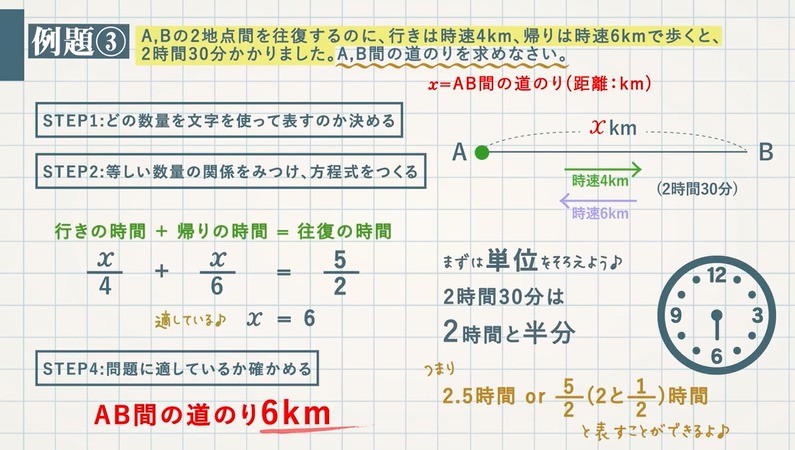
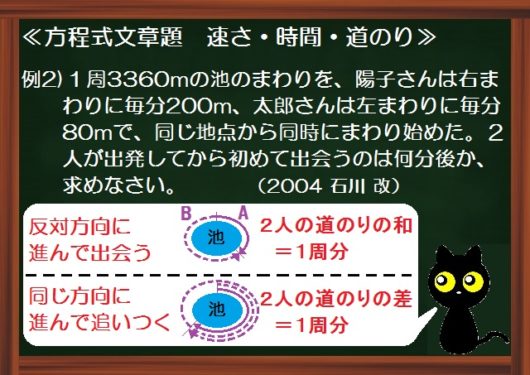
距離・速さ・時間(復習) まずは復習として距離・速さ・時間の関係を復習しておきましょう。 これらを関係を使う文章題にチャレンジしましょう。 例題①池のまわりに 1 周 3000 m の遊歩道がある。 A,Bが同じ地点から互いに反対方向にスタートし 例題1 藤原君の家からデパートまでの距離は6kmある。自転車を使って分速1mで移動すると何分かかるか? 速さ・時間・距離のそれぞれの関係は以下の式で表すことができます。 距離=速さ×時間 速さ=距離÷時間 時間=距離÷速さ これらの式が覚えにくい場合は、下の図を活用して 距離=速さ×時間ですから、 65x55x=480 この方程式を解けばよいわけです。 65x55x=480 1x=480 x=4 答えは4分後です。 (2)2人が同じ方向に歩き出すと、AがBをはじめて追いこすのは出発して何分後か。 追いつく時間をx分後とします。




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




文章題 速さ 追いつく1
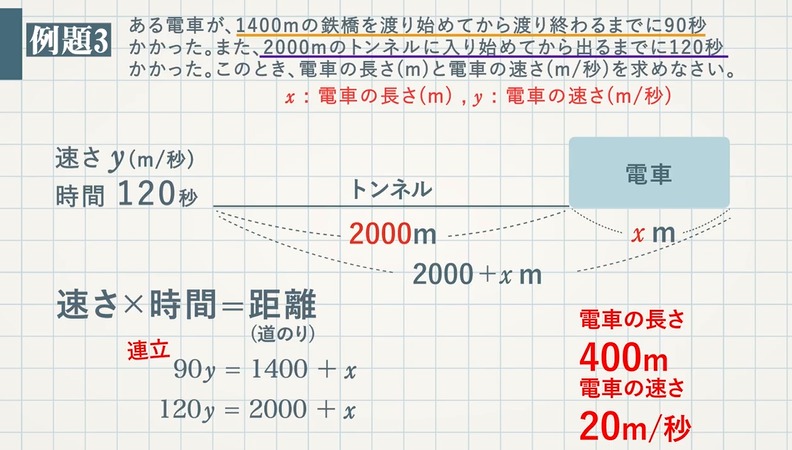
時間×速さ=道のり ①X分×分速70m ② (20-X)分×分速150m ①の道のり+②の道のり=1.8 km (1800 m)速さ・道のり・時間 速さとは、 「単位時間に進んだ道のり」 である。 そこから公式を導くことができる。 公式 速さ= 道のり 時間 、 道のり=速さ×時間、 時間= 道のり 速さ 例 400mの道のりを歩くのに5分かかった。 旅人算、通過算、流水算は全て"速度、距離、時間"のいわゆる"速さ"計算の応用です。 そこで、基本となる式が下記です。 距離(道のり) = 速度(速さ) x 時間 特に速さの問題を特にあたり



3




数基礎 Com 追いつく旅人算が分かる方法
式) 32÷8 = 04(時間後) 時間を 分に変換するためには60倍すればよい。 04時間を分に変換すると、 式) 04×60 = 24(分後) よって、MがLに追いつくのは、Mが出発してから24分後である。 Mが出発するのは、Lが出発した40分後の11時15分なので、追いつくのアンケートにご協力頂き有り難うございました。 送信を完了しました。 旅人算(追いつく時間) のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業100x=80x480 x=480 x=24 問題13 分速 100 mで歩く弟が家を出発してから 6 分後に兄が分速 250 mの自転車で追いかけた. (1) 兄が出発してから追いつくまでの時間を x 分とおいて,兄が分速 250 mの自転車で進む距離を左辺に,弟が分速 100 mで 6 分多く歩いて進む




Spi非言語の速さ 時間 距離の問題です Clear
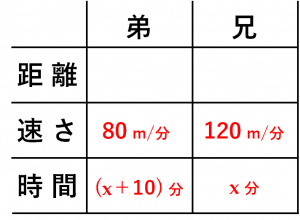



中1数学 方程式 方程式の利用 速さの文章題は表を使おう たけのこ塾 勉強が苦手な中学生のやる気をのばす
今回は時間や距離、速さの公式についておさらいをしてみましょう。ちなみに、このときの時間は朝の10時です。 spi spi対策損益計算 挑戦!練習問題! 前回学習した損益計算の練習問題。全部で2問あります。 最初に追いつく時間(t)=一周÷速さの差 二回目以降に追いつく時間も同じ →t×1,t×2,t×3 (時間) に追いつきを繰り返す 最初に追いつく距離(d)=t×速さ ニ回目に追いつくまでの距離も同じ →スタート地点からd×1,d×2,d×3の距離で 追い付きが繰り返される追いつく旅人算二人の差で時間・速度・距離の計算する 例1) 時速$40km$で走っている軽自動車の$5km$後ろに、パトカーが時速$45km$で走っていました。 このパトカーが軽自動車に追いつくのは、何分後ですか。 まずはこの文章から数字の部分を抜き出してみましょう。




時間 距離 速さ 数的推理 すれちがい算 追いつく 公務員試験道場




はじき 速さ 距離 時間を1次方程式で求める問題 Youtube
速80m,弟は分速180m で進むとするとき,次の各問いに答えよ。 (1) x次の表は,弟が出発してから 分後に兄に追いつくとして数量の関係をまとめたもので ある。表の①~③に数式を入れよ。文章題 (速さ) 「追いつく1」 注意点 表にまとめる 求めるものをxにする。 先に出た人と後から出た人の 距離は同じ 。 歩いていた (走っていた)時間は 先に出た人のほうが長い 。 例題 弟が家を出て毎分80mで歩いて行った。 兄がその5分後に毎分100m



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S6 004 Pdf




何分後に追いつくでしょう 妹が分速50メートルで家を9時に出発し 数学 教えて Goo
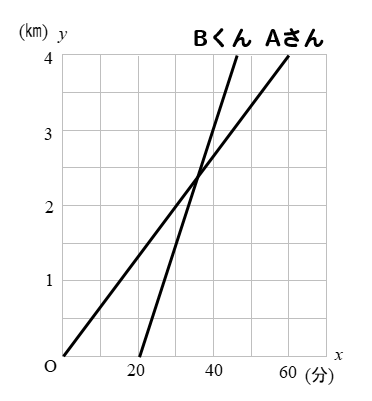



一次関数の利用 追いつく速さの文章問題を解説 数スタ




方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




3 Descubre Como Resolverlo En Qanda




一次関数の利用 追いつく速さの文章問題を解説 数スタ




中1数学 方程式の文章題 速さ 例題編 映像授業のtry It トライイット



旅人算 2人が追いつく問題の解き方は 数スタ
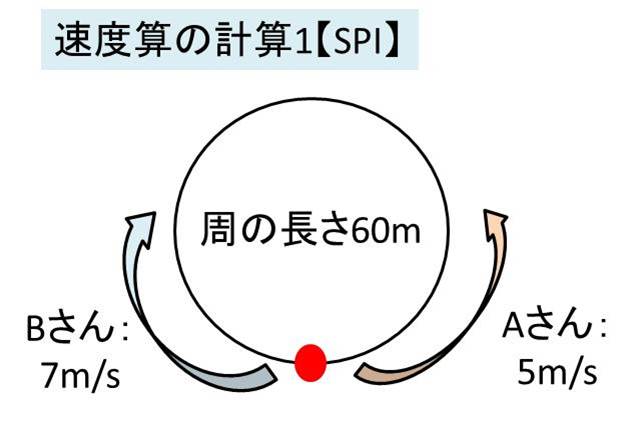



Spi 速度算 旅人算 の計算を行ってみよう 追いつき算
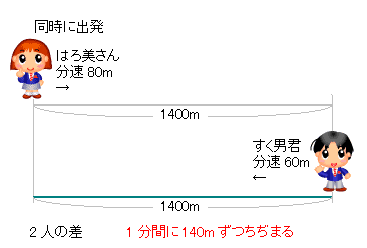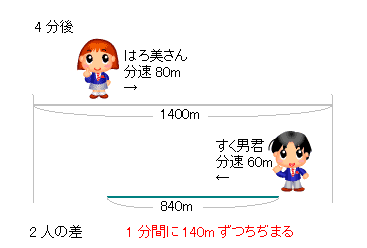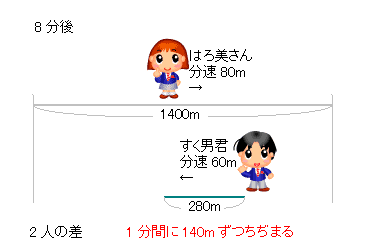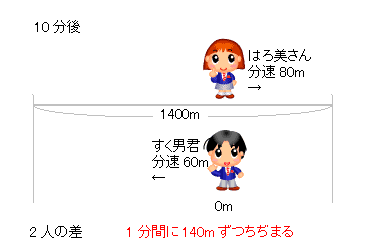



旅人算
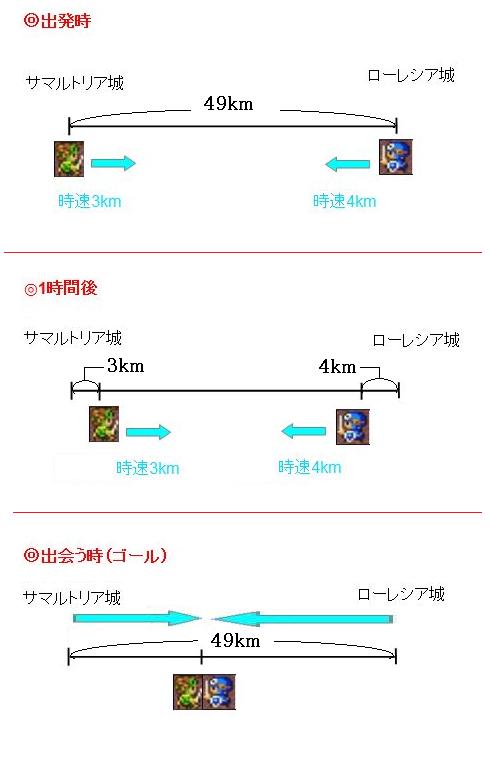



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける
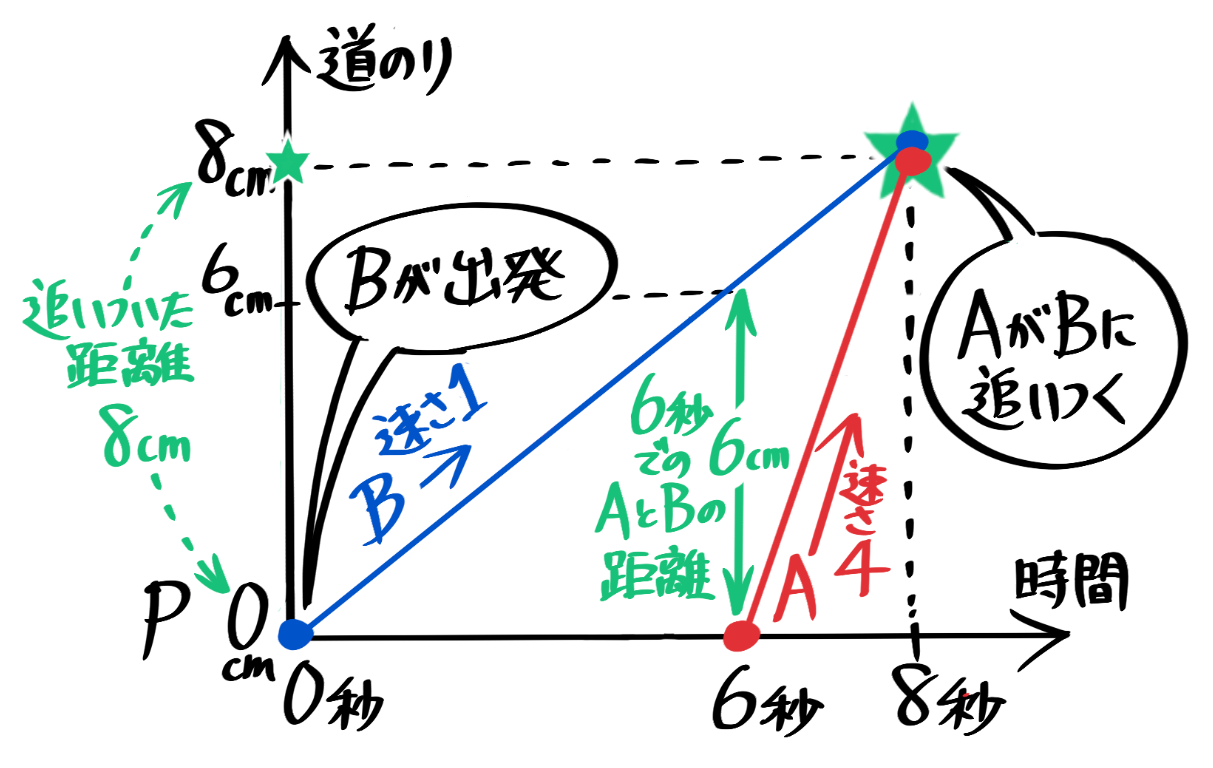



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ




一次方程式 道のり 速さの文章問題 追いつく系 の解き方 Qikeru 学びを楽しくわかりやすく




苦手克服 方程式で速さの文章題を攻略する3つのコツ Qikeru 学びを楽しくわかりやすく




方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト



連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ




一次方程式 道のり 速さの文章問題 追いつく系 の解き方 Qikeru 学びを楽しくわかりやすく



無料 中1数学 基本解説 問題プリント 方程式5 方程式の利用3 127




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス
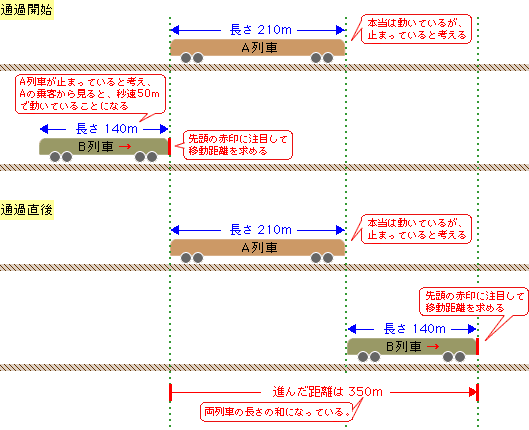



通過算 算数の教え上手 学びの場 Com



3
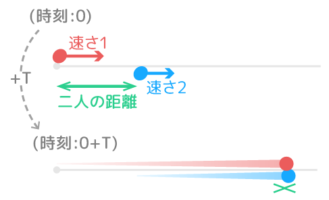



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ




時間の比と速さの比 なぜ逆にするんですか Clear




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校



文章題3 規則集7 中学から数学だいすき
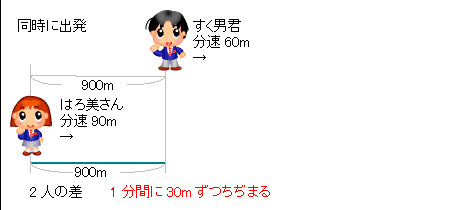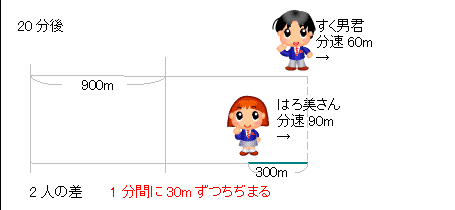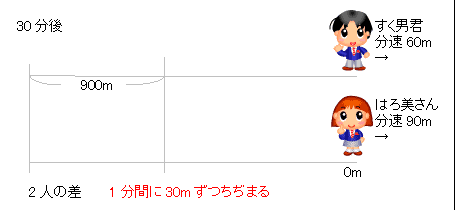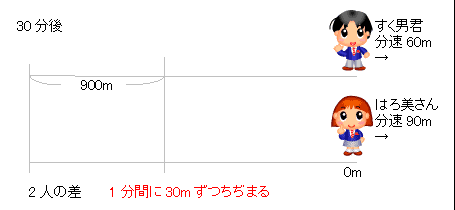



旅人算



方程式の利用 文章題 距離 速さ 時間 教遊者



旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather



連立方程式の利用 距離 速さ 時間 教遊者




方程式利用 何分後に追いつくか 速さの文章問題を徹底解説 数スタ



最高のコレクション 速さ 時間 距離 はじき ニスヌーピー 壁紙



一次方程式 道のり 速さの文章問題 追いつく系 の解き方 Qikeru 学びを楽しくわかりやすく




Spi非言語問題 速さ 時間 距離 問題のポイント 就活の答え




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり その2




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学



Mathematics 1次方程式の利用 3 速さ 食塩水の問題 働きアリ




算数 速さ道のり 追いつき算 旅人算 Youtube



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S6 006 Pdf



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




旅人算 2人が追いつく問題の解き方は 数スタ




数的推理が面白いほどわかる講義 37 旅人算 Youtube




方程式の利用 文章題 距離 速さ 時間 教遊者




旅人算の基本 図をかいて整理しよう




速さ の文章問題 計算ドリル 問題集 数学fun



1



速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




方程式の解き方 道のり編 Youtube



方程式の利用 文章題 距離 速さ 時間 教遊者



2



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学




中1 数学 文字と式8 速さ 時間 距離 16分 Youtube




旅人算 Wikipedia



1




基本 一次方程式の利用 速さ なかけんの数学ノート



千葉県公立高校入試 数学 距離 速度 時間を求める問題 17年前期第2問 3 11年後期第2問 3 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー
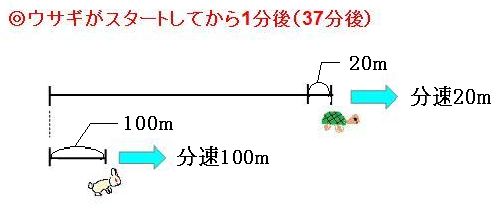



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算 池の周りで追いつく問題の解き方 考え方 算数パラダイス
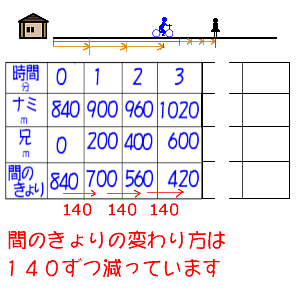



6年算数 変わり方を調べて 1 追いつき算
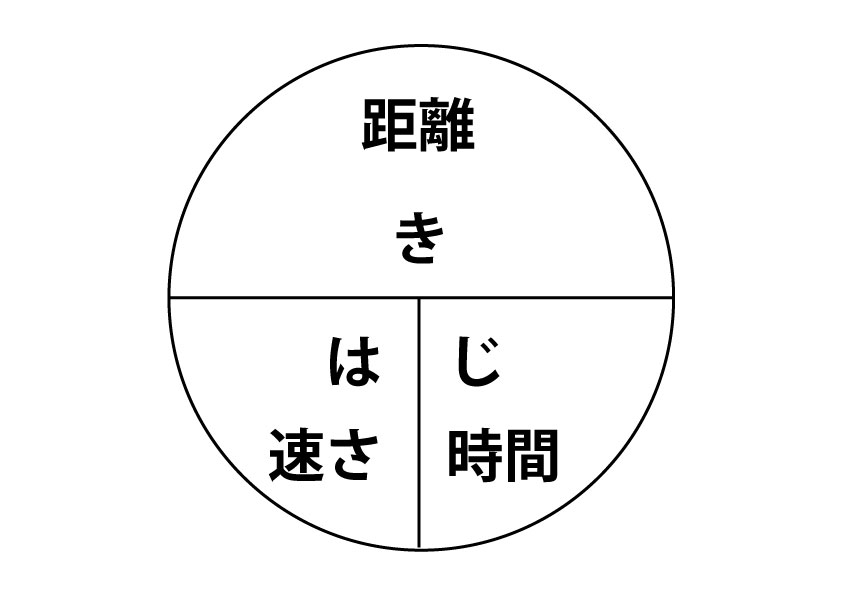



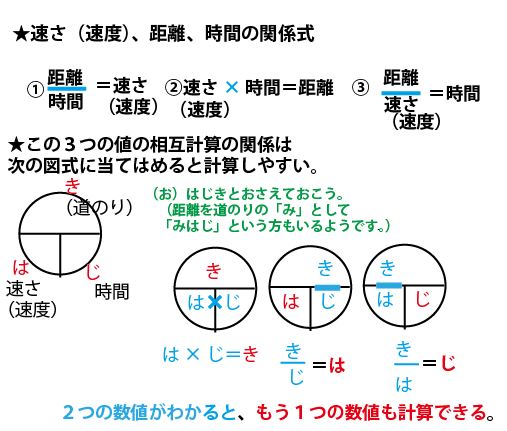
はじき みはじ の法則 速さ 時間 距離 簡単な公式の覚え方 Yattoke 小 中学生の学習サイト
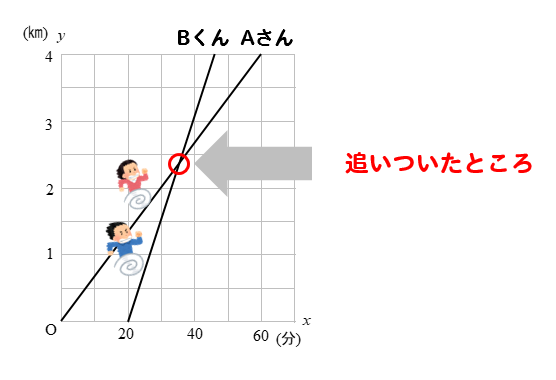



一次関数の利用 追いつく速さの文章問題を解説 数スタ
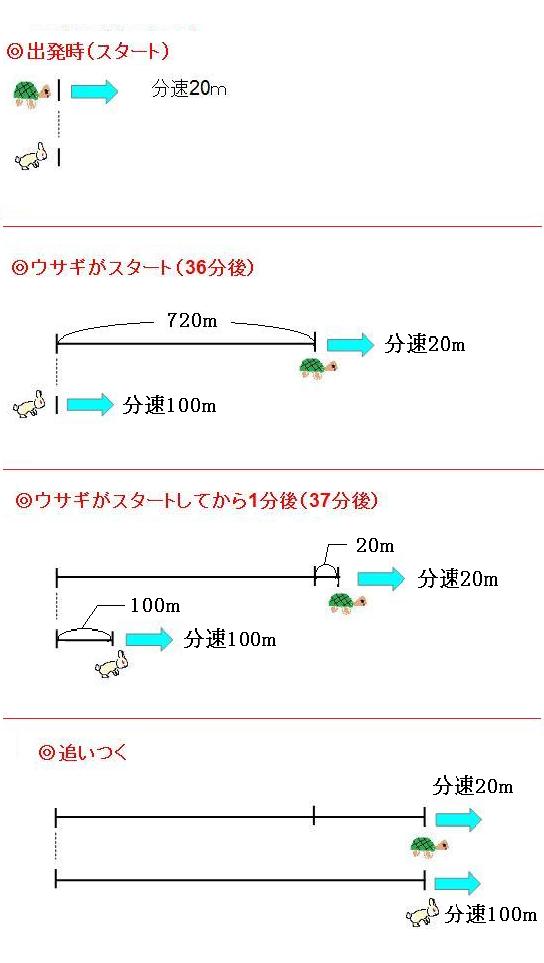



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




みんなの知識 ちょっと便利帳 ある距離を ある速度で進んだ時にかかる時間は 距離 速度 時間を計算する 移動した距離 時速 時間 などを求めることができます




数基礎 Com 追いつく旅人算が分かる方法




方程式の利用 文章題 距離 速さ 時間 教遊者
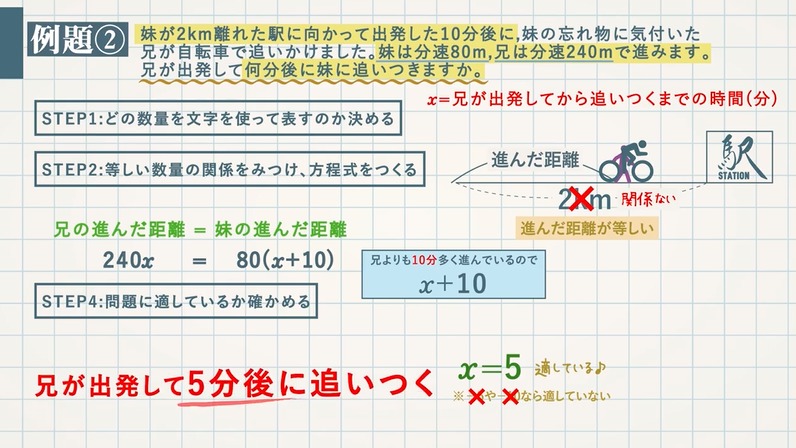



方程式の利用 文章題 距離 速さ 時間 教遊者
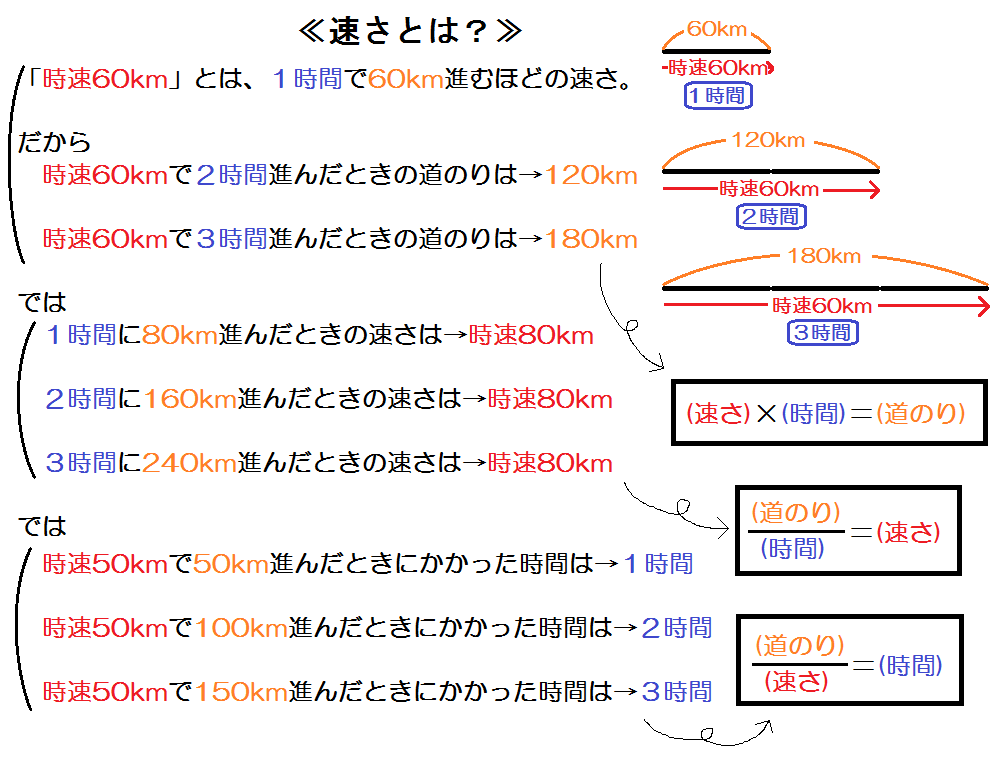



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
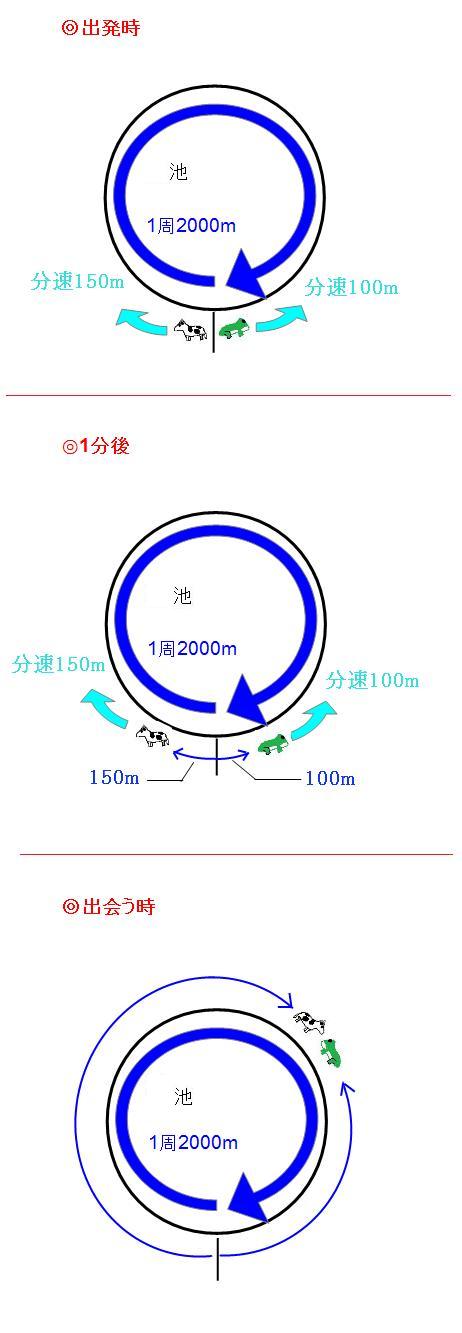



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




連立方程式 池の周りを同じ方向 反対方向に回る問題を解説 Youtube




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月



1次方程式 速さ 中学から数学だいすき
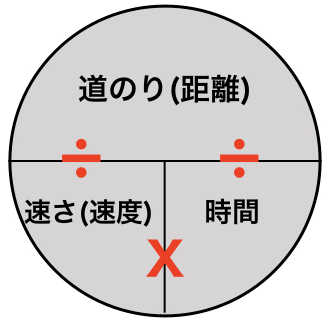



速度計算 速度 距離 時間と速さ 道のり 時間の覚え方攻略 Landgather




中一数学 方程式 での速さ 追いつく時間 に関する問題




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
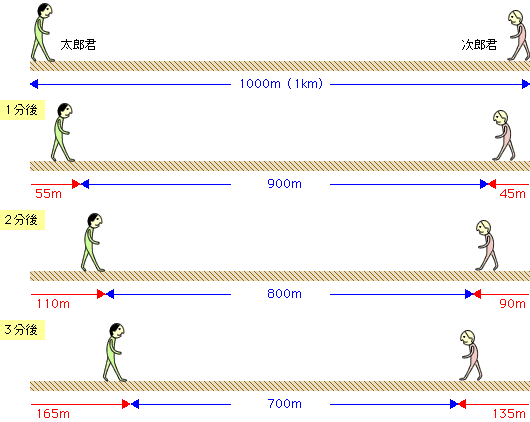



旅人算 算数の教え上手 学びの場 Com




Spi非言語の速さ 時間 距離の問題です Clear




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



旅人算 追っかけ問題 追い越し




基本 一次方程式の利用 速さ なかけんの数学ノート
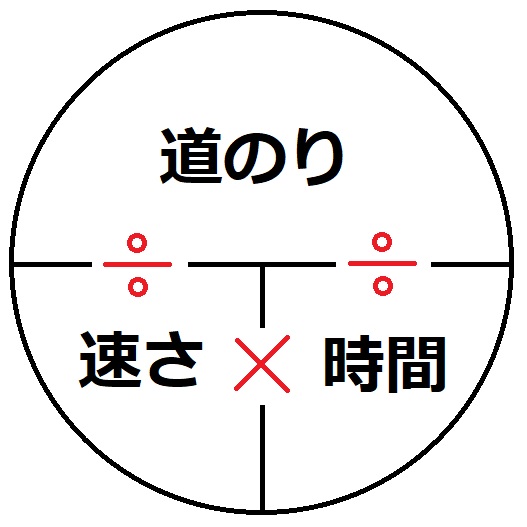



基本 旅人算の解き方 テクニック 中学受験 塾なし の勉強法



6年算数 変わり方を調べて 1 追いつき算



0 件のコメント:
コメントを投稿